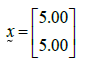حل نظم المعادلات الغير خطية في الماتلاب Solving NonLinear Systems of Equations

 حل نظم المعادلات الغير خطية في الماتلاب 

المعادلات الخطية Linear Equations هي معادلات من الدرجة الاولى يمكن وضعها على الصورة aX = b وهي صورة معادلة الخط المستقيم. حيث a مصفوفة المعاملات، X مصفوفة المتغيرات، b مصفوفة الحدود المطلقة وفيما يلي امثلة للمعدلات الخطية :

3x1 + 2x2 – 2x3 = 7 2x1 + 5x2 – 2x3 = 4 5x1 – 6x2 + 7x3 = 19

بينما المعادلات الغير خطية قد لا تكون من الدرجة الاولى او معادلات على الصيغة الاسية او المثلثية والتي يصعب احيانا فصلها وحلها بالطرق التقليدية للمعادلات الخطية لذلك تستخدم طرق التحليل العددي مثال طريقة نيوتن رافسون وفيما يلي امثلة على نظم المعادلات الغير خطية:

x1²+x2²=50
x1x2=25
او
x1³+x2²+5x3=5
x1x2+x3³=15
2x1+3x2⁵+e^x3
او
sin(x1)-sin(x2) = 0
cos(x1)-cos(x2) = 0

سنتعرف على كيفية حل المعادلات الغير خطية في الماتلاب بطريقتين : 

1 - الاولى هل طريقة نيوتن رافسون في الماتلاب

2 - الثانية باستخدام مكتبة symbol و دالة solve في الماتلاب  

1 - حل المعادلات باستخدام طريقة نيوتن رافسون 

ذكرنا في الموضوع السابق كيفية حل وايجاد جذور المعادلة الجبرية باستخدام طريقة نيوتن رافسون وفيما يلي مراجعة وشرح لكيفية استخدام طريقة نيوتن رافسون :

2 - حل المعادلات باستخدام الدوال الجاهزة في برنامج الماتلاب مكتبة symbol و دالة solve في الماتلاب 

يمكن حل المعادلات الغير خطية باستخدام مكتبة الSymbolic واستخدام الدالة Solve كالتالي :

[x1,x2,..,xN] = solve([eqs], [vars])

مثال لحل المعادلتين الآتيتين:

2x₁² + x₂² = 0
x₁ - x₂  = 5

نستخدم الكود التالي :

syms x1 x2
f1 = 2x1^2 + x2^2
f2 = x1 - x2 -5
[x1s , x2s] = solve([f1, f2] , [x1, x2])

حيث ان x1s, x2s هي قيم x1, x2 التي تحقق حل المعادلات السابقة.
ايضا يمكن اهمال المتغيرات وتمرير المعادلات f1, f2 فقط الى الدالة solve كالتالي :

[x1s , x2s] = solve(f1, f2)

مثال (1) حل نظم المعادلات الغير خطية التالية باستخدام طريقة نيوتن رافسون :

Example (1) Write a program in any programming language (i.e. matlab, fortran etc.) you prefer that gives the approximate solution of the following non-linear system of equations using the iterative procedure of Newton-Raphson method:

x₁² + x₂² - 50 = 0
x₁x₂ - 25 = 0

solution:
f1= x₁² + x₂² - 50
f2= x₁x₂ - 25

The Jacobian can be calculated as:
Considering an initial solution: x1=0 , x2=1

x = [ 0 ; 1]

We can calculate the solution as:

xi+1 = xi - J-1.f(xi) = xi - Δxi

the solution of the system is:

كود برنامج الماتلاب لحل معادلات مثال (1) باستخدام نيوتن رافسون:
Example (1) Newton Raphson Matlab Code:
clear all; clc;
%iteration number of substitutions
N=100;
%Assume Error tolerance  = 0.00001 = 10^-5 = 1e-5
ErrTol = 1e-5;
syms x1 x2           %define x1 x2 as symbols variable
f1 = x1^2+x2^2-50;   %define first equation of x1 and x2
f2 = x1*x2-25;       %define second equation of x1 and x2
fs = [f1; f2];       %define the array(function) of functions f1 and f2
%define array of symbols for the variable
xs = [x1; x2];
%calculate the jacobian for the array of functions fs
jac = jacobian(fs,xs);
%set initial value for iteration x1=0, x2=1
x = [0 ; 1]; 
%for loop to iterate from 1 to N=100 and substitute values
for i=1:N
        f = double(subs(fs, xs, x));  %f here equal fs(xi)
        j = double(subs(jac,xs, x));  %j here equal jac(xi) 
        x = x - inv(j)* f;            %sub in newton Raphson equation  
    
        %compute and tolerate the error 
        err = abs(inv(j)* f);
        if(err < ErrTol )
                break;
        end
end
display(x);

كود برنامج الماتلاب باستخدام الدالة Solve لحل معادلات مثال (1) :
%define variable
syms x1 x2 
%define equations f1 and f2
f1 = x1^2+x2^2-50;
f2 = x1*x2-25;
%solve the two equation and store in 2D matrix 
%x1s for x1 values and x2s for x2 values
[x1s, x2s] = solve(f1,f2);
%[x1s,x2s] = solve([f1,f2], [x1 x2])  %equavalent to the above


مثال (2) حل نظم المعادلات الغير خطية التالية باستخدام طريقة نيوتن رافسون في الماتلاب :
Example (2) Write a matlab program that computes the approximate solution of the following system for each value of t  where t = 0: 0.1: 1
sin(x1) - sin(x2) - cos t = 0
cos(x1) - cos(x2) - sin t = 0
solution:
f1= sin(x1) - sin(x2) - cos t
f2= cos(x1) - cos(x2) - sin t 
state with intial value x=[0, 1] for x1,x2
let error tolerance 10-5 
t = 0: 0.1: 1
كود برنامج الماتلاب لحل معادلات مثال (2) باستخدام نيوتن رافسون:
Example (2) Newton Raphson Matlab Code:
clear all; clc;
%number of iteration for newton Raphson
N=100;
%Error tolerance 
ErrTol=1e-5;
syms x1 x2 t             %define variables x1, x2 and t as symbols
f1 = sin(x1) - sin(x2) - cos t;  %f1 define first equation of x1 and x2
f2 = cos(x1) - cos(x2) - sin t ; %f2 define Second equation of x1 and x2
fs = [f1; f2];            %fs define the array(function) of functions f1 and f2
%xs define the array of symbolic variables 
xs = [x1;x2];
%calculate the jacobian for the array of functions fs
jac = jacobian(fs,xs);
%set range of values for p1
t = 0:0.1:1;    
%x define the solution matrix of (x1,x2) for every value of t
x = zeros(max(size(xs)),max(size(t))); 

%first 'for' iterate for every value of t
for m = 1:max(size(t)) 

    %substite the value of t at each iteration
    fp = subs(fs, {'t'}, {t(m)});
    
    %initial value of variables at every iteration of t
    xp = [0 ; 1]; 
    %second 'for' iterate for newton Raphson calculations 
    for i=1:N   
        f = double(subs(fp, xs, xp)); %fm(xp)
        j = double(subs(jac,xs, xp)); %jac(xp)   
        xp = xp - inv(j)* f  ;        %newton Raphson formla 
        
        %compute and tolerate the error 
        err = abs(inv(j)* f);
        if(err < ErrTol)
            break;
        end
    end
    
    x(:,m) = xp;
end
display(x);

كود برنامج الماتلاب باستخدام الدالة Solve لحل معادلات مثال (2) :
syms x1 x2 t
f1 = sin(x1) - sin(x2) - cos t;
f2 = cos(x1) - cos(x2) - sin t ;
[x1s, x2s] = solve(f1,f2); 
%[x1s, x2s] = solve([f1,f2] , [x1, x2]); 
x1s = double( subs(x1s,{t},{0:0.1:1}) );
x2s = double( subs(x2s,{t},{0:0.1:1}) );
display(x1s);
display(x2s);

مثال (3) حل نظم المعادلات الغير خطية التالية باستخدام طريقة نيوتن رافسون في الماتلاب :
Example (3) Write a program that computes the approximate solution of the following system for each value of p1,p2 where :
x12 + x22 = p1
x1x2 = p2
p1 = 0: 5: 50 
p2 = 0:2.5:25
solution:
f1= x12 + x22 - p1
f2= x1x2 -p2
state with intial value x=[0, 1] for x1,x2
let error tolerance 10-5 
كود برنامج الماتلاب لحل معادلات مثال (3) باستخدام نيوتن رافسون:
Example (3) Newton Raphson Matlab Code:
clear all; clc;
%number of iteration for newton Raphson
N=100;
%Error tolerance 
ErrTol=1e-5;
syms x1 x2 p1 p2 %define variables x1, x2 and p1, p2 as symbols
f1 = x1^2+x2^2-p1; %f1 define first equation of x1 and x2
f2 = x1*x2-p2;     %f2 define Second equation of x1 and x2
fs = [f1; f2];     %fs define the array(function) of functions f1 and f2
%xs define the array of symbolic variables 
xs = [x1;x2];
%calculate the jacobian for the array of functions fs
jac = jacobian(fs,xs);
%set range of values for p1
p1 = 0:5:50;    
%set range of values for p2
p2 = 0:2.5:25;  
%x define the solution matrix of (x1,x2) for every p1,p2 values
x = zeros(max(size(xs)),max(size(p1))); 

%first 'for' iterate for every (p1, p2) value
for m = 1:max(size(p1)) 

    %substite for each value of (p1,p2,..) at each iteration
    fp = subs(fs, {'p1','p2'}, {p1(m), p2(m)});
    
    %initial value at every iteration of p1,p2
    xp = [0 ; 1]; 
    %second 'for' iterate for newton Raphson calculations 
    for i=1:N   
        f = double(subs(fp, xs, xp)); %fm(xp)
        j = double(subs(jac,xs, xp)); %jac(xp)   
        xp = xp - inv(j)* f  ;        %newton Raphson formla 
        
        %compute and tolerate the error 
        err = abs(inv(j)* f);
        if(err < ErrTol)
            break;
        end
    end
    
    x(:,m) = xp;
end
display(x);

كود برنامج الماتلاب باستخدام الدالة Solve لحل معادلات مثال (3):

syms x1 x2 p1 p2 f1 = x1^2+x2^2-p1; f2 = x1*x2-p2; [x1s, x2s] = solve(f1,f2); %[x1s, x2s] = solve([f1,f2] , [x1, x2]); x1s = double(subs(x1s,{p1,p2},{0:5:50, 0:2.5:25})); x2s = double(subs(x2s,{p1,p2},{0:5:50, 0:2.5:25}));

display(x1s);

display(x2s);